| |
|
|
| |
Los
geómetras
|
|
| |
Un debate imaginario ha sido construido con extractos de fuentes históricas
de distintas épocas. Tiene que ver con la forma de una sección cónica
en particular. Léanlo con atención:
Serenus:
Como se que muchos expertos geómetras piensan que la sección transversal
del cilindro es diferente de aquella del cono que se llama elipse, he
pensado que no se les debe permitir cometer esa equivocación. Es absurdo
que los geómetras hablen de un problema geométrico sin dar pruebas, y
que sean atraídos por apariencias de verdad, en contra del espíritu de
la geometría. Sin embargo, como ellos están convencidos de aquello y yo
de lo contrario, lo probaré "more geométrico" que ambos sólidos tienen
una sección del mismo tipo, más bien idéntica, tal que el cono y el cilindro
sean cortados de un modo apropiado. (Las secciones del cilindro y Las
secciones del cono IV D.C.)
|
|
| |
|
|
| |
Witelo:
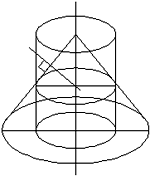
Todas las elipses que son secciones del cono de ángulo agudo son más grandes
en el lado próximo a la base del cono: esto no es verdadero en aquellas
obtenidas como secciones del cilindro. Esto pasa por la polaridad (agudez)
del cono y la regularidad del cilindro. De hecho, por otra parte, consideremos
la intersección del eje del cono con una línea perpendicular a un lado del
triángulo axial; si trazamos un círculo en el cono con ese centro e imaginamos
un cilindro con ese circulo como base: es evidente que la porción inferior
de la sección cónica es externa al cilindro, mientras que la parte superior
de la sección cilíndrica contiene la parte superior de la sección cónica.
Por otro lado, las dos partes de la sección cilíndrica son iguales por la
regularidad del sólido y la equivalencia angular con el eje. De ahí se deduce
la tesis. (Sobre perspectiva, 1200 D.C.) |
|
| |
 |
|
| |
|
|
| |
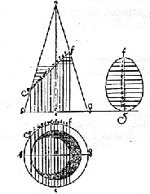
Durero:
No conozco los nombres germanos para las secciones (cónicas), pero sugiero
llamar a la elipse, curva en forma de huevo, ya que es idéntica a él. (Tratado
sobre la medición con regla y compás sobre líneas, planos y cualquier cuerpo,
1525) |
|
| |
 |
|
| |
|
|
| |
Guidin:
Es necesario evitar el error de aquellos que piensan que la elipse (cónica)
es más angosta en la parte más cerca del vértice del cono y más ancha en
la parte más próxima a la base del cono: por el contrario son muy similares
(Centrobaryca, 1640) |
|
| |
|
|
| |
Traducción
de Which is the shape of an ellipse? A cognitive analysis of an historical
debate. Autores: Maria Bartolini Bussi, Maria Alessandra Mariotti. |
|
| |
|
|
| |
Volver
a Documentos |
|
| |
|
|

